Mivel a média tele van az újinfluenzáról - a következőt vajon hogy fogják hívni? egyébként a szezonális influenza is általában a sertésektől jön - szóló hírekkel, ebben a bejegyzésben főleg arról szeretnék írni, hogyan lehet kiszámolni, hogy hányan fognak összesen megbetegedni a járványban. A vírus genetikai vizsgálata nyomán kutatók úgy becsülték, hogy a most terjedő A/H1N1 reprodukciós száma kb. 1.2. A korai mexikói adatok 1.4-1.6-ot mutattak, míg Új-Zélandon (ahol most tél van) és Japánban egészen 2-ig felment ez a szám. De mit is jelent ez a számunkra?
Korábban már leírtam, mit jelent a reprodukciós szám fogalma: R0 azt fejezi ki, hogy egy fertőző egyed várhatóan hány másodlagos fertőzést generál összesen egy teljesen fogékony populációban. Ha például R0=3, akkor egy Mexikóból hazatért fertőzött turista várhatóan 3 polgártársunkat fogja megfertőzni, akik egyenként további hármat-hármat, és így tovább. Ha R0<1, akkor nem lesz járvány. A reprodukciós szám függ egyrészt az adott vírustól, valamint az adott populációtól is, ahol terjed. Sőt, ez változik is, hiszen a 
háttérben egy kegyetlen háború zajlik az emberiség és a vírusok között: mi próbálhatjuk csökkenteni a reprodukciós számot a betegek elkülönítésével, gyógykezeléssel, vakcinálással, védőmaszkok kiosztásával, iskolák és zsúfolt helyek bezárásával (Izraelben repülő csodarabbikat is bevetnek, de attól tartok, a vírust ez kevéssé hatja meg). Ugyanakkor a sertésinfluenza vírusa további mutációkkal növelheti a reprodukciós képességét, ahogy egyre jobban adaptálódik az emberhez. Szórványosan már előfordultak az antivirális szerekre rezisztens esetek is.
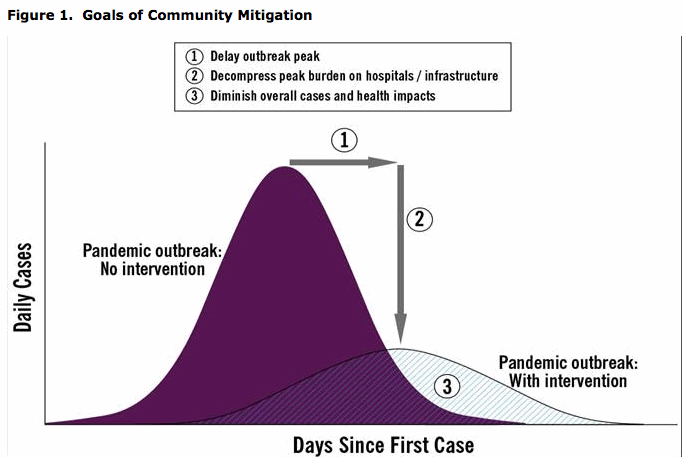
Egyértelmű tehát a cél, csökkentsük 1 alá a reprodukciós számot! De még ha nem is tudjuk 1 alá vinni , akkor is érdemes csökkenteni, mint azt az alábbi ábra is szemlélteti, de ennél kicsit konkrétabbat is mondhatunk.
Van ugyanis egy viszonylag egyszerű (közelítő) matematikai összefüggés, ami a járványterjedési modellek jórészében teljesül (és viszonylag egyszerűen le is vezethető, de ettől most itt eltekintek), ami a reprodukciós szám függvényében megmondja, hányan fognak megbetegedni a járvány teljes ideje alatt összesen:
log(S*) = R0 x (S*-1),
ahol S* azok aránya, akik egyáltalán nem betegedtek meg a járvány alatt a fogékony emberek közül, vagyis 1-S* azok aránya, akik megbetegedtek. Ezt úgy hívják, hogy végállapot-egyenlet, é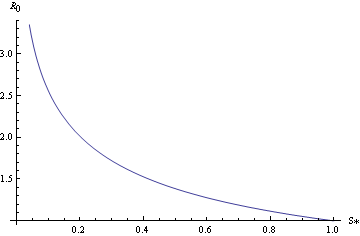
s azt adja, hogy még R0=1.15 esetén is képes egy populáció kb. egynegyedét megfertőzni. Ez persze csak akkor történhetne, ha
egyrészt karba tett kézzel ülnénk, másrészt a populáció teljesen védtelen lenne. 1.15-ös R0-t viszonylag könnyen 1 alá lehet csökkenteni, és a spanyolnátha esete is mutatja, hogy már az akkori intézkedéseknek köszönhetően is drasztikusan kevesebben betegedtek meg (becslések szerint a teljes népesség 25%-ával), mint amit a fenti összefüggés ad. A mellékelt ábrán látható, hogy mi történne a reprodukciós szám függvényében, ha semmit nem tennénk a járvány ellen.
Néhány napos hír, hogy a kormány 6 millió vakcinát rendelt 6 milliárd forintért, ami minden bizonnyal elegendő, ha tényleg hatékony, hiszen a 60%-os immunitási arány elvileg még egy 2.5-ös R0-t is meg tud állítani. Kanada még ennél is jobban túlbiztosítja magát, ott a 75%-os immunitás a minimum elvárás és a 34 millió lakosnak 50 millió vakcinát vettek 400 millió dollárért.
