Bizonyára sokan emlékeznek még középiskolából arra a feladattípusra, amikor minél kevesebb mérésből kell kitalálni, melyik ládában van az igazi kincs. Ennek nagyon sok változata van (egykarú és kétkarú mérleggel is), és ezek nagyon jó kis logikai fejtörők, de valószínűleg kevesen gondolták, hogy ennek köze lehet valami gyakorlati problémához. Pedig igen, és ezt a szifilisz-tesztelés példájával fogom illusztrálni.
A szifilisz egy elég csúnya fertőző nemi betegség, ha máshol nem is, az iskolában Ady Endre kapcsán mindenki hallott már róla. Az antibiotikumoknak köszönhetően nagyrészt sikerült visszaszorítani, de az elmúlt évtizedben ismét emelkedett az esetek száma több fejlett országban, így az Egyesült Államokban is. Az amerikai hadseregben is újra gondokat okoz a szifilisz. Tegyük fel, hogy mindenkit le akarnak tesztelni, hogy kiszűrjék a fertőzötteket, de egy szifiliszteszt nagyon drága. Hogyan lehet minél olcsóbban megoldani az egész hadsereg letesztelését? Ezt a problémát már konkrétan megoldották a második világháború idején is.
Az alapötlet nagyon egyszerű: a szifiliszt vérmintából tesztelik, így egybeönthetjük egy csomó ember vérét, és teszteljük ezt. Ha a minta negatív, akkor az adott csoportban senki sem szifiliszes, így további tesztre nincs szükség. Ha pozitív, akkor a csoportban van legalább egy szifiliszes, ez esetben a csoport minden tagját leteszteljük. Mivel a szifilisz viszonylag ritka, arra számíthatunk, hogy ha az embereket csoportosítva teszteljük, akkor sok csoport tesztje ad negatív eredményt, így megspórolunk jó sok tesztet, hiszen ezen csoportok tagjait nem kell külön letesztelni. A matematikai feladvány meghatározni azt, hogy mekkora csoportokat alakítsunk ki, hogy a lehető legkevesebb tesztből megtaláljuk az összes szifiliszest.
Legyen $N$ a tesztelendő populáció létszáma és $x$ az egyes csoportok létszáma, tehát lesz $\frac{N}{x}$ csoportunk. Ha $x$ túl kicsi (szélsőséges esetben $x=1$, amikor mindenkit egyenként tesztelünk), akkor a csoportok nagy száma miatt sok tesztet kell végeznünk. Ha $x$ túl nagy, akkor pedig várhatóan minden csoportban akad majd szifiliszes így minden csoport tesztje pozitív lesz. Az várható tehát, hogy van egy köztes, optimális csoportméret. Ki tudjuk-e ezt számolni?
Van $\frac{N}{x}$ csoportunk, tehát ennyi tesztet mindenképpen el kell végeznünk. Legyen $p$ annak a valószínűsége, hogy egy véletlenszerűen kiválasztott személy szifiliszes (vagyis $p$ a szifilisz gyakorisága a populációban). Ekkor $(1-p)^x$ a valószínűsége, hogy egy $x$ fős csoportban senki sem az, ekkora eséllyel lesz a minta negatív, tehát $1-(1-p)^x$ eséllyel pozitív. Ha a minta pozitív, akkor a csoport minden tagján, összesen tehát $x$ számú további tesztet végzünk. A pozitív mintájú csoportok várható száma $\frac{N}{x}(1-(1-p)^x)$. Az összes tesztek számát tehát az $\frac{N}{x}(1+(1-(1-p)^x)x)$ formula adja meg, ennyi tesztet elvégezve megtalálhatjuk az összes szifiliszest. Ebből $N$-et kiemelhetjük, így kapjuk, hogy az
$f(x)=\frac{1}{x}+1-(1-p)^x $
függvényt kéne minimalizálnunk. Vegyük észre, hogy az optimális $x$ nem függ $N$-től, úgyhogy azzal nem is foglalkozunk a továbbiakban, csak feltesszük, hogy egy elég nagy szám (hogy ki tudjunk alakítani $x$ fős csoportokat). Függ viszont a $p$-től, ami érthető, hiszen ha a szifilisz nagyon gyakori, akkor más csoportméret lehet az optimális, mint ha nagyon ritka lenne.
Az $f(x)$ függvény minimumát explicit módon is kifejezhetjük $p$ függvényében, bár kissé komplikált (lásd itt, a $W$ a ProductLog vagy más néven a Lambert-féle W-függvényt jelenti). Konkrét $p$ értékre viszont egyszerűen kiszámolhatjuk numerikusan is. A CDC adatai szerint az USA-ban 100 000 emberből 15.4 szifiliszes, ami $p$=0.000154-et jelent. A Minimize[{1/x + 1 - (1 - 0.000154)^x, x > 0}, x] Mathematica parancs rögtön kiadja nekünk, hogy ehhez a $p$ értékhez 81 fős csoportok az optimálisak, és ekkor $f$ értéke 0.0247431, ami azt jelenti, hogy elegendő a populáció 2.47%-ának megfelelő számú tesztet végezni, ahelyett, hogy mindenkit egyenként letesztelnénk.
Tehát egy kis matematikával 97,5%-ot spórolhatunk.
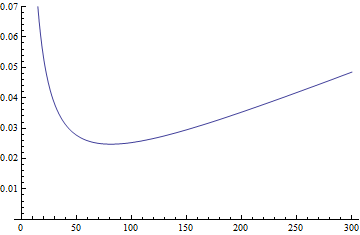
Az ábrán az $f$ függvény grafikonja látható $p$=0.000154 esetben. Észre lehet venni, hogy az optimális $x$=81 nagyon közel van az ${1}/{\sqrt{p}}$=80.6-hoz. Ezt egy heurisztikával is levezethetjük: $f$ minimalizálásához válasszuk $x$-et úgy, hogy a két tag, ${1}/{x}$ és $1-(1-p)^x$ egyenlő legyen. Ha $x={1}/{\sqrt{p}}$, akkor $p={1}/{x^2}$, vagyis $1-(1-p)^x=1-(1-x^{-2})^x$. Most az $(1-x^{-2})^{x^2/x} \approx e^{-1/x} \approx 1-1/x$ közelítésből kapjuk, hogy $1-(1-p)^x$ is kb. $1/x$. Vagyis az optimális csoportméretet így közelíthetjük $x={1}/{\sqrt{p}}$-vel, $f$ minimuma pedig $2/x=2\sqrt{p}$ ami a $p$=0.000154 esetben a 0.02482, elég pontos közelítést adja.
Ezt a módszert lehet még javítani is, ha rekurzívan alkalmazzuk. Tehát először csoportokra osztjuk a populációnkat, majd a pozitív eredményűeket újra kisebb csoportokra osztjuk, és így tovább. Legyen házi feladat, hogy meddig lehet így elmenni.
forrás: Jeffrey Shallit Recursivity blog
