Korábban már írtam egy bejegyzést Fabrice Bellard π-rekordjáról. Most egy japán-amerikai páros, Shigeru Kondo és Alexander Yee jelentette be, hogy ennél is sokkal tovább jutott. Az új rekordról az MTI is hírt adott (lásd pl. itt és itt), meglehetősen alacsony színvonalon.

Új Pi-rekordnak örülhet a világ: két informatikus 5 billió tizedesjegyig pontosította a kör kerületének és átmérőjének hányadosát. A korábbi csúcs januárban született: egy brit matematikus, Fabrice Bellard közel 2,7 billió tizedesig haladt az osztással.

Miféle osztással haladt Bellard? A fenti két mondat alapján mintha a hír szerkesztője úgy képzelné a dolgot, hogy veszünk egy kört, aztán a kerületét elosztjuk az átmérőjével és csak osztunk, osztunk, és osztunk...

A π nagy pontosságú kiszámításához általában a Chudnovsky-formulát használják: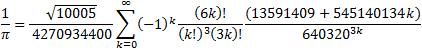

 Egy jó kis gyűjtemény található π-formulákról a Mathworld oldalán. Míg Bellard egy átlagos hétköznapi számítógépen érte el a rekordját, az új eredményhez erősebb gépet használtak, a technikai részletek itt olvashatók. Aki maga szeretne kiszámolni néhány százezer vagy millió számjegyet, az elindulhat innen.

De van még ennél szörnyűbb rész is az MTI-hírben:

A Pi azért érdekes, mert nem ismétlődik számsor a kapott hányadosban.

 Ez így szinte minden szinten rossz. Eltekintve attól, hogy idegesítő módon "a kapott hányados"-ként hivatkozik a π-re, ez a mondat a maga pongyola módján nyilván azt akarja kifejezni, hogy a π végtelen tizedestört alakja nem szakaszos, vagyis a π irracionális szám (amit 1761-ben bizonyítottak). Nos a π nem éppen ezért érdekes, hiszen irracionális számok vannak dögivel. A π a számjegyeiben megbúvó mintázatokon (illetve azok hiányán) túl azért érdekes, mert fontos szerepe van a matematika szinte minden ágában: a geometria, az analízis, a valószínűségszámítás, a számelmélet, de még a kombinatorika (lásd Stirling formula) sem tud meglenni nélküle. Csakúgy mint a kozmológia, a kvantummechanika, az elektromosságtan, vagy a relativitáselmélet. A minket körülvevő univerzum lényegéhez tartozik. És még külön magyar blogja is van.