Nemrég olvastam az alábbi matematikatörténeti érdekességet egy könyvben [1], amely szerint elképzelhető, hogy a legnevezetesebb fraktál, a Mandelbrot-halmaz eredetét Szegeden kell keresni.
[1] Tóth J., Simon L.P., Differenciálegyenletek, Typotex 2005

1952-ben a magyar nyelvű Matematikai Lapok feladatrovatában a szegedi Riesz Frigyes (a valaha élt egyik legnagyobb magyar matematikus) az alábbi problémát tűzte ki:
" Milyen z1 komplex számokból kiindulva ad adott komplex a mellett a zn+1 = (1/2)(zn2 + a) iteráció konvergens sorozatot?"
Két évvel később Hajós György, a feladatrovat szerkesztője ezt írta: "Az 54. feladatra, melyet szerzője a megoldást nem ismerve tűzött ki, megoldás nem érkezett. Ha a jövőben megoldás érkezik erre a feladatra, azt közölni fogjuk."
Benoit Mandelbrot éppen ilyen iterációk tanulmányozása nyomán vezette be a fraktál fogalmát.
- No de mi a kapcsolat a Matematikai Lapok és Benoit Mandelbrot között? - kérdezheti teljes joggal az olvasó. Mandelbrot volt Princetonban Neumann János utolsó posztdoktori kutatója, és az ottani könyvtár, a Fine Hall Library megkapta a magyar nyelvű Matematikai Lapokat, amit minden bizonnyal Neumann is szívesen lapozgatott, Mandelbrot pedig Neumanntól kapta a kutatási problémáit. Természetesen ez csak spekuláció, nem lehetünk benne biztosak, hogy valóban Riesztől Neumannon át jutott el a probléma Mandelbrotig, de könnyen elképzelhető. Talán csak maga Mandelbrot tudná megmondani, miért is kezdett ezzel a kérdéssel foglalkozni. A Fractals and Chaos című könyv előszavában felsorolja azokat a matematikusokat, akik nagy hatással voltak rá, és Neumannt nem említi, azt viszont igen, hogy az ötvenes évek elején kezdett munkája teljesedett ki végül a hetvenes évek végén a fraktálok elméletével.
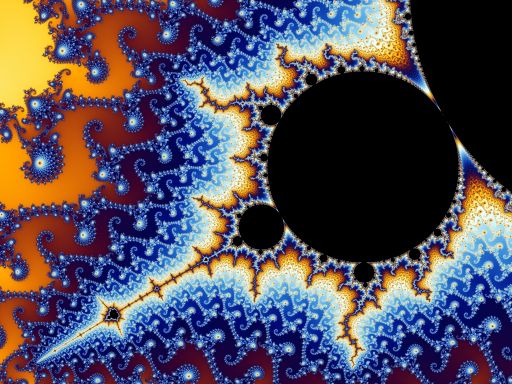
A képeken látható Mandelbrot-halmaz azon c komplex számokból áll (itt elolvasható, hogyan kell komplex számokkal számolni), amelyekre a zn+1 = zn2 + c komplex másodfokú polinom iterálásával kapott, a 0 pontból induló sorozat korlátos (vagyis tudunk rajzolni a komplex síkra egy olyan kört, hogy a sorozat minden eleme a körön belül lesz). Ez tehát a 0, c, c2 + c, (c2 + c)2 + c, ... sorozat. Könnyen látható, hogy ha például c=3, akkor a sorozat (0,3,12,147,...) a végtelenbe tart, tehét a 3 az nincs benne a Mandelbrot-halmazban. Ellenben ha c=i (a képzetes egység), akkor a kapott sorozat 0, i, (−1 + i), −i, (−1 + i), −i…, ami korlátos, tehát i eleme a Mandelbrot-halmaznak. Ha feketére színezzük azokat a pontokat a komplex számsíkon, amelyek a Mandelbrot-halmaz elemei, akkor a fenti fekete-fehér ábrát kapjuk. Az alábbi színes képeket (ráklikkelve meg lehet őket nézni nagyobb felbontásban) olyan algoritmusok generálják, amelyek aszerint színezik a pontokat, hogy a hozzájuk tartozó sorozat mennyire gyorsan vagy lassan nő.
Ez az egyik legegyszerűbb nemlineáris diszkrét dinamikai rendszer, mégis ez az egyszerű szabály egy fantasztikusan gazdag struktúrát határoz meg. A fraktál szó a latin fractusból (töredezett) ered, és általában olyan önhasonló halmazokat jelent, amelyek tetszőleges kicsi skálán nézve is ugyanolyan szerkezetet mutatnak, vagyis ha erősen "rázoomolunk", akkor is hasonló dolgokat látunk. A fraktálokról és a kapcsolódó színezési algoritmusokról, programokről óriási mennyiségű információ található az interneten.
Végül egy video a Mandelbrot-halmaz nagyításáról: